Development of a Novel Growth Model Based on the Central Limit Theorem for the Determination of Beef Spoilage
Applied Food Biotechnology,
Vol. 8 No. 2 (2021),
16 March 2021
,
Page 143-150
https://doi.org/10.22037/afb.v8i2.33549
Abstract
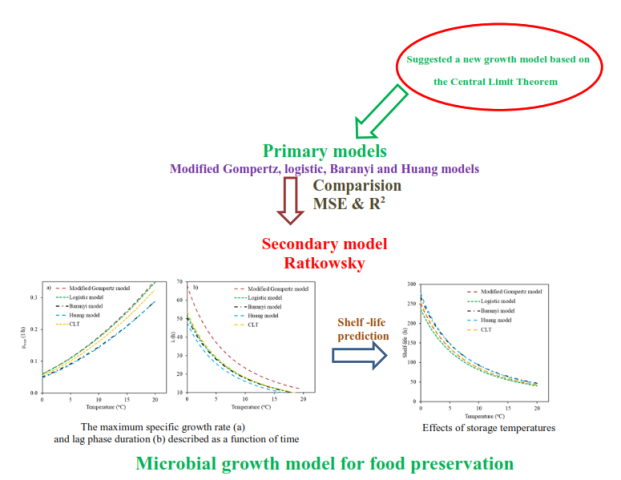
Background and Objective: Currently, no published studies are available that compare central limit theorem model with traditionally used growth models in predictive food microbiology to describe bacterial growth behaviors of Pseudomonas spp. in beefs. The major objectives of the present study were to develop a novel growth model based on the central limit theorem and compare the prediction capability of the model with those of various growth models (modified Gompertz, logistic, Baranyi and Huang models) commonly used in predictive food microbiology.
Material and Methods: Bacterial growth data for Pseudomonas spp. were collected from previously published studies on beefs stored at isothermal storage temperatures (0, 4, 7, 10, 15 and 20 °C). Temperature dependent kinetic parameters (maximum specific growth rate ‘µmax’ and lag phase duration ‘λ’) collected from various primary models were described as functions of storage temperatures using Ratkowsky model. Fitting capability of the novel growth model based on the central limit theorem was compared with other growth models using mean square error and coefficient of determination.
Results and Conclusion: The novel growth model developed in this study provided mean square errors less than 0.104 and coefficients of determination greater than 0.962. No significant differences (p>0.05) were seen between the statistical indices of this developed model and traditionally used growth models. Results have shown that the novel growth model based on the central limit theorem can be used to describe the growth behaviors of microorganisms as alternative to traditionally used growth models of modified Gompertz, logistic, Baranyi and Huang models in predictive food microbiology. Furthermore, this novel model can be used for the prediction of shelf-life of beefs as a function of temperature since spoilage of beefs is directly linked to the load of Pseudomonas spp.
- ▪ CLT
- ▪ growth kinetic
- ▪ microbiological quality
- ▪ predictive microbiology
- ▪ shelf-life
How to Cite
References
Buchanan, R.L., Whiting, R.C., Damert, W.C., 1997. When is simple good enough: a comparison of the Gompertz, Baranyi, and three-phase linear models for fitting bacterial growth curves. Food Microbiol. 14, 313-326.
Huang, L., 2008. Growth kinetics of Listeria monocytogenes in broth and beef frankfurters Determination of lag phase duration and exponential growth rate under isothermal conditions. J. Food Sci. 73(5), E235-242.
Huang, L., 2017. IPMP Global Fit–A one-step direct data analysis tool for predictive microbiology. Int. J. Food Microbiol. 262, 38–48.
Kreyenschmidt, J., Ibald, R., 2012. Modeling shelf life using microbial indicators. In: Nicoli, M.C. (Ed.), Shelf life Assessment of Food. CRC Press, New York, pp. 127-168.
Pérez-Rodríguez, F., Valero, A., 2013. Predictive Microbiology in Foods. Springer, New York.
Ratkowsky, D.A., Olley, J., McMeekin, T.A., Ball, A., 1982. Relationship between temperature and growth rate of bacterial cultures. J. Bacteriol. 149, 1-5.
Robazza, W.D., Teleken, J. T., Galvão, A. C., Miorelli, S., Stolf, D. O., 2017. Application of a model based on the central limit theorem to predict growth of Pseudomonas spp. in fish meat. Food Bioprocess Tech. 10, 1685-1694.
Robinson, T.P., Ocio, M.J., Kaloti, A., Mackey, B.M., 1998. The effect of the growth environment on the lag phase of Listeria monocytogenes. Int. J. Food Microbiol. 44, 83-92
Whiting, R.C., 1995. Microbial modeling in foods. Crit. Rev. Food Sci. 35, 467–494.
Zhang, Y., Mao, Y., Li, K., Dong, P., Liang, R., Luo, X., 2011. Models of Pseudomonas growth kinetics and shelf life in chilled Longissimus dorsi muscles of beef. Asian Austral. J. Anim. 24, 713-722.
Zwietering, M.H, Jongenburger, I., ombouts, F.M, van’t iet, K., 1990. Modeling of the bacterial growth curve. Appl. Environ. Microb. 56, 1875–1881.
- Abstract Viewed: 435 times
- pdf Downloaded: 520 times
